Термин «Направленность» возник в среде аудиофилов и меломанов в 1970х годах. Именно тогда люди впервые заговорили о том, что симметричные с точки зрения физики аудио кабели и провода оказывается вовсе не симметричны и каким-то образом изменяют звук аудио системы при смене направления их включения. Вплоть до середины 2000х считалось, что Направленность свойственна только электрическим проводникам. Большинство при этом было уверено, что направление проводников имеет значение только в сигнальных цепях, однако продвинутые аудиофилы ориентировали даже сетевые кабели, выбирая лучшее по звуку положение вилки в розетке, их считали сумасшедшими. Ориентация проводников в усилителях и пояснения причин выбора того или иного направления много лет были достаточно бессистемными, в 2005 году направленность проводников в сигнальных цепях и цепях питания усилителей наконец была систематизирована.
Систематизация направлений, наряду с отбором компонентов по специфическим критериям и выбором экстремально простой конструкции позволила создать необычный Тестовый Аудиотракт (ТА), благодаря которому появилась возможность определять музыкальные свойства отдельных радиодеталей и проводов с недостижимой до этого точностью. Довольно быстро выяснилось, что направление предпочтительного звучания компонентов практически никогда не совпадает с длинной стороной деталей. Даже у проводов, отношение длины к толщине у которых необычайно велико, наилучшее звучание всегда получалось при касании определенных точек на боковых поверхностях. Чтобы описать такое положение вещей был введен термин Векторная Направленность.
Термины
Векторная Направленность — термин показывающий, что Направленность — это трехмерный, а не линейный (одномерный) феномен, как это считалось ранее.Векторная Ориентация — соединение деталей аудиосистем с учетом направлений их векторов.Внутренняя (Врожденная) Направленность (ВН) — это Направленность (Вектор), сформированный в процессе производства (металл, пластик) или рождения (дерево, камень) материала, из которого изготовлен компонент. см. Формирование Вектора.Поверхностная Направленность (ПН) — это дополнительный к ВН Вектор меньшей силы и значительно меньшей устойчивости. ПН состоит из нескольких простых векторов последовательно возникающих при механической обработке, химических реакциях (окисление), окраске и лакировке поверхности.Вектор — это отрезок прямой, проходящей сквозь тело компонента, начинающийся в определенной точке входа на поверхости компонента и заканчивающийся в определенной точке выхода. Вектор описывает трехмерное направление наиболее ясного звучания радиокомпонента (его входные и выходные точки) и ориентировочную выраженность (силу) его направленности. Общий Вектор компонента равен векторной сумме ВН и ПН и изменяется во времени всвязи с дрейфом силы и направления ПН.Вектор Вращения (ВВ) — определяет поступательное и тангенциальное направление навивки проводника относительно продольного направления детали, на которую навивается проводник см. ниже.Радиус Вектор — радиальная проекция Вектора, образующаяся в многослойных катушках индуктивности и рулонах конденсаторов, см. ниже. В природе присущ всем растениям (см. рис 4).-
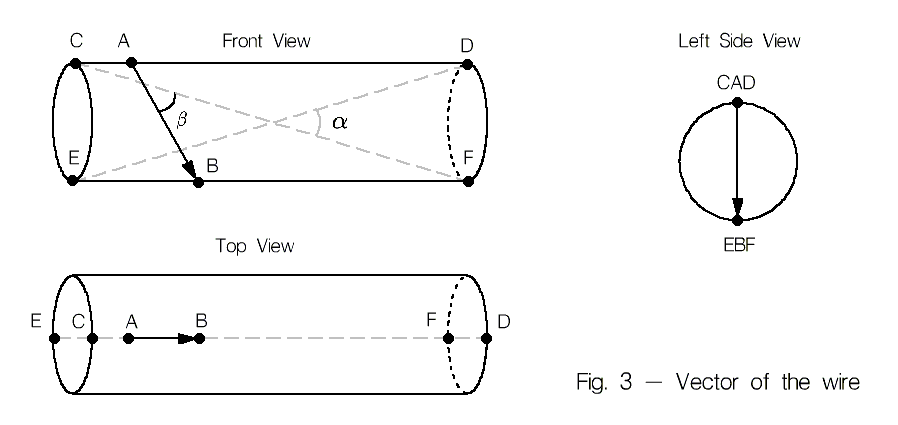
Вектор Фантом — Вектор \overline{AB}, пересекающий воздушное пространство, возникшее между точками A и B в процессе изменения формы детали. Подробнее здесь. Векторные Потери — ухудшение ясности звучания аудиотракта, связанное с не точным соблюдением векторной направленности его компонентов при монтаже. Потери зависят от величины угла \beta рис.3 между вектором и линией, проведенной между точками соединения компонента в электрическую цепь.Векторное Поле — поле неизвестной природы, формирующее векторную направленность у металлов и диэлектриков в момент их перехода из жидкого состояния в твердое. Наличие Векторного поля выведено гипотетически.Ясность — везде, где не указано обратное имеется ввиду Музыкальная Ясность — субъективная (тонкая) характеристика звучания, тесно пересекающаяся с понятием Несомость звука — критерием из лексики скрипичных мастеров и специалистов по акустике помещений. Улучшение ясности часто воспринимается как появление «водуха», разборчивости звучания отдельных инструментов оркестра и точности в их интонациях. Экспериментально установлено, что потери ясности нарастают с добавлением каждого нового компонента, провода либо неточного соединения в тракте, поэтому ясность — это единственный устойчивый ориентир при выборе правильного направления компонента.
Определение направления вектора
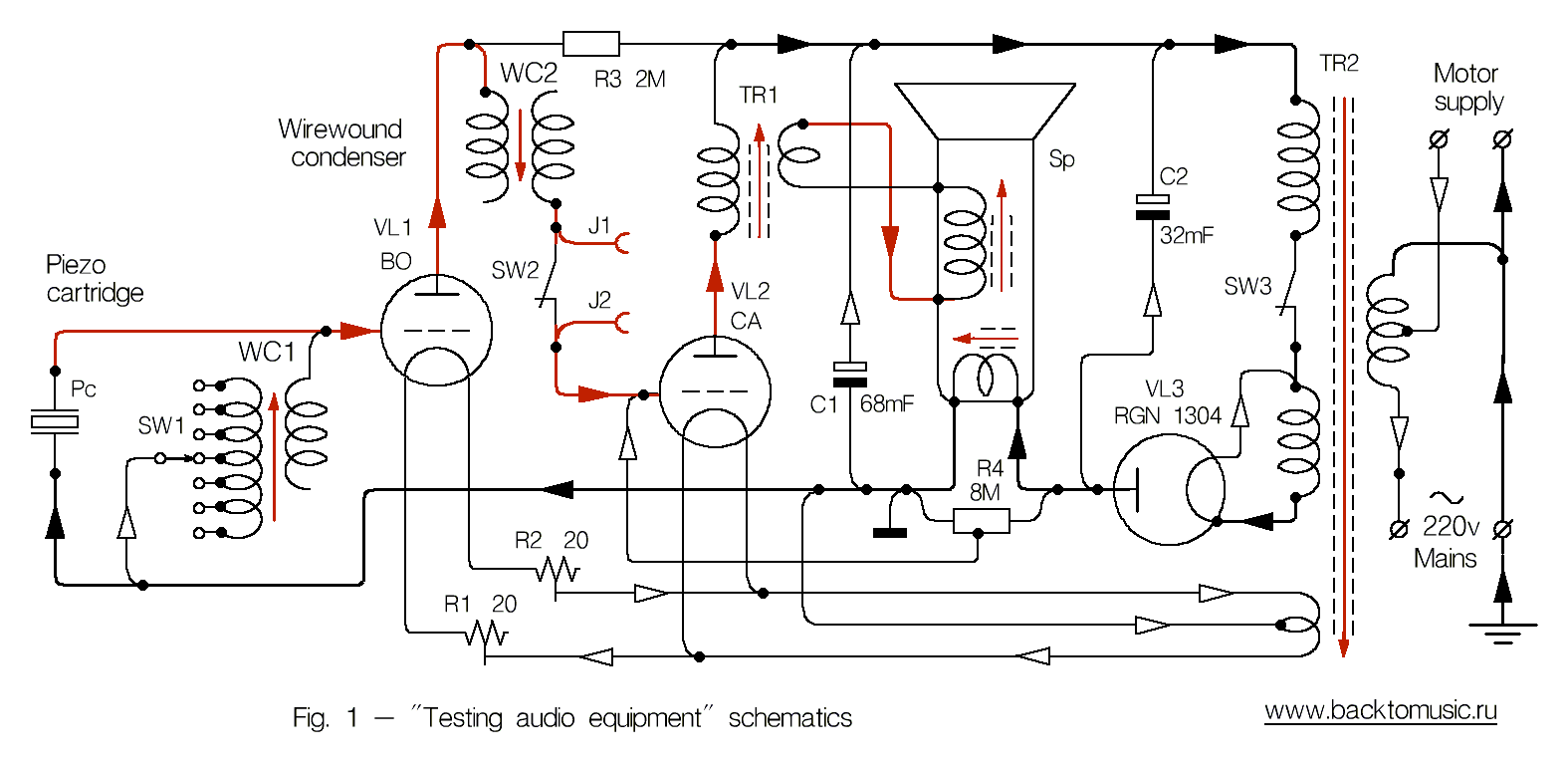
Классический метод — тестируемый компонент включается в разрыв сигнальной цепи Тестового Аудиотракта (ТА) несколькими различными способами, изменения звучания тракта оцениваются на слух и выбирается наиболее ясный вариант. Замыкание сигнальной цепи через тестируемый компонент происходит с помощью длинных тестовых щупов J1 и J2 (см. схему рис.1), установленных в разрыве соединения между проволочным конденсатором WC2 и сеткой выходной лампы Siemens CA. Высокое входное сопротивление лампы СА позволяет тестировать не только провода, но и конденсаторы, индуктивности и даже диэлектрики, если их поверхность смочена водой. При этом небольшое усиление оконечного каскада позволяет использовать в качестве щупов длинные провода без экранов, ухудшающих ясность звучания системы.
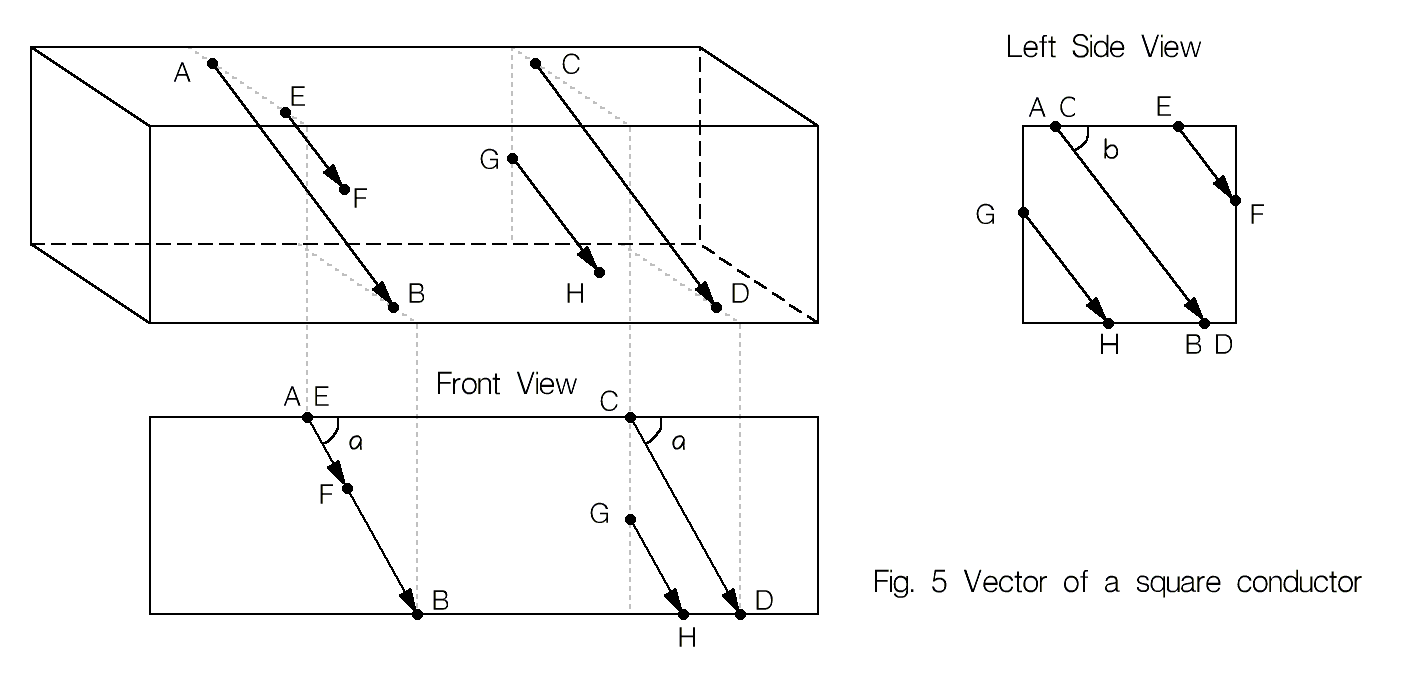
На рис. 3 вектор \overline{AB}— это направление наилучшего звучания провода, определенное с помощью Тестового Аудиотракта. C, D, E, F — практически возможные точки электрического контакта провода с соседними компонентами. На практике наилучший реультат будет при контакте вдоль вектора \overline{CF}, наихудший — через \overline{FC}, варианты \overline{ED} и \overline{DE} — промежуточные. Не зная этих особенностей, можно легко ошибиться во время тестирования провода, поскольку хоть \overline{ED} и \overline{DE} по направлению почти противоположны, звучат они примерно одинаково тк оба находятся под большим углом к \overline{AB}. В случае тестирования провода через эти точки вероятность правильного определения направления провода близка к 50%. Интересно, что в длинном проводе угол a становится практически равным нулю, то-есть \overline{CF} становится практически равным \overline{ED}, а \overline{FC} — равным \overline{DE}, однако вышеперечисленные особенности звучания короткого отрезка провода так же хорошо проявляют себя и на длинном куске.
* — Во избежание ошибок во время тестов необходимо учитывать направление вектора щупов Тестового Аудиотракта.
Экстрасенсорный (тактильный) вариант
Направленность — это феномен, не поддающийся привычному логическому анализу. Стороннему человеку вообще сложно поверить, что кто-то может чувствовать изменения в звучании, вносимые одним единственным проводом на фоне тысяч предположительно аналогичных по силе влияний, существующих в самом тракте и существовавших в процессе записи аудио носителя. Скептики справедливо обращают внимание на этот факт. На мой взгляд, аудиофильская сверхчувствительность сродни сверх обонянию некоторых животных, например самец бабочки Saturnia pavonia, ощущает запах феромона самки в радиусе 11 км. Если учесть, что концентрация вещества в воздухе с увеличением расстояния падает в кубе, то вероятность обнаружения хотя бы одной молекулы крохотного источника ферамона уверенно стремится к нулю. Однако самец как-то чувствует свою пару, точно так же, думаю, и меломаны остро чувствуют некие тонкие мелизмы, до которых обычным людям нет никакого дела. И судя по всему, механизмы этой чувствительности куда как тоньше тех, о которых нам рассказывают на уроках биологии.
Тонкость аудио-вибраций подтверждает интересный факт — качество Окраски и Направление компонента можно оценить не только на слух, но и с помощью осязания. В начале исследований для тестов использовался только Тестовый Аудиотракт, как описано выше, мне и в голову не могло прийти, что музыкальный потенциал деталей и проводов можно оценить как-то иначе, чем на слух. ТА исправно выполнял свои функции несколько лет, пока однажды во время сборки магнитопровода трансформатора не случился знаменательный инциндет — перед началом теста катушка была подпаяна к разъемам J1 и J2 (схема рис. 1), но выключатель SW2 остался замкнутым, то-есть сигнал проходил напрямую в сетку лампы минуя щупы. Работа проводилась как обычно: ш-пластина вставлялась в катушку четырьмя возможными способами, на слух выбиралось ее лучшее положение, затем процесс повторялся со следующей пластиной и так далее. Замкнутый выключатель был обнаружен только после окончания сборки: музыка продолжила играть когда выводы катушки были отпаяны от J1 и J2. Ситуация недвусмысленно намекала на то, что все обнаруженные различия были просто самовнушением и это был удар ниже пояса. Однако впечатления во время тестов были абсолютно реальны, в этом я мог поклясться и мне пришло в голову, что щупы соединенные с усилителем каким-то образом могли, например, играть роль антенны. Было решено перепроверить результат — пластины были помечены краской, затем магнитопровод разобран и собран в слепую по новой с разомкнутым SW2. Новый результат на 80% совпал с предыдущим! Моему удивлению тогда не было конца, но это было только начало.
Следующий удивительный момент открылся в процессе поиска ответа на вопрос, каким образом в классическом тесте проводников с ТА могут возникать серийные ошибки. Например, при массовом тестировании с помощью ТА при перепроверке результатов 10 раз результат мог быть правильным, потом подряд могло быть 5 неправильных результатов потом опять шли правильные. После долгих мучений стало очевидно, что причиной большинства ошибок были мои руки, а именно каким образом удерживались щупы во время тестирования. Мои руки оказались энергетически несимметричными, левая рука была выраженным выходом, а правая — входом. Системные ошибки ушли в прошлое, когда выходной щуп J1 стал удерживаться в левой руке, а J2 — в правой.
Через какое-то время я столкнулся с совсем уж невероятным фактом — оказалось, что для определения направления щупы вообще не нужны — включив музыку можно было просто повертеть деталь в руках и найти ее наиболее естественное положение между ладонями или пальцами. Перепроверка на ТА показывала, что в этом случае со стороны левой руки располагалось начало компонента, а со стороны правой — конец. Это была эмоциональная встряска сокрушительной силы.
Следущее открытие окончательно перевернуло все с ног на голову — во время очередных тактильных тестов я случайно обнаружил, что музыку при этом включать вообще не обязательно, направление и общий музыкальный потенциал детали так же уверенно можно было ощутить и в полной тишине. Шах и Мат материализму.
Свойства векторов
- Векторная направленность свойственна всем твердым предметам, как созданных человеком, так и необработанным, природным материалам.
- Направленность проявляет себя не только в аудио, но и в оптике.
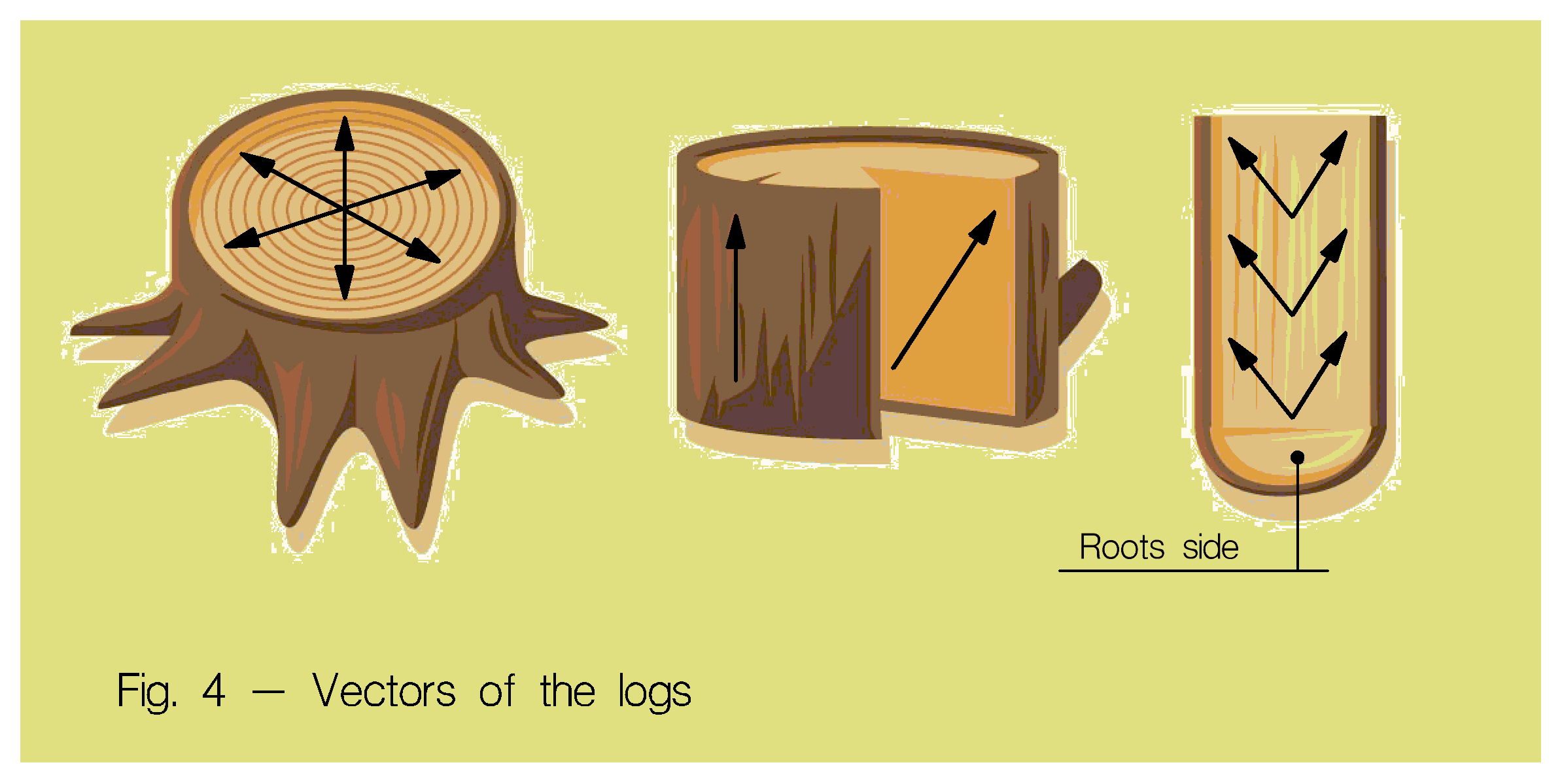
- У растений вектор направлен в соответствии с изменениями их размеров во время их роста, то-есть — от корней к кроне и от сердцевины к поверхности (рис. 4).
- Совпадение направления вектора фабрично изготовленного компонента с его продольной осью – редкий, частный случай. Прямой связи вектора с геометрической формой фабричных компонентов не обнаружено.
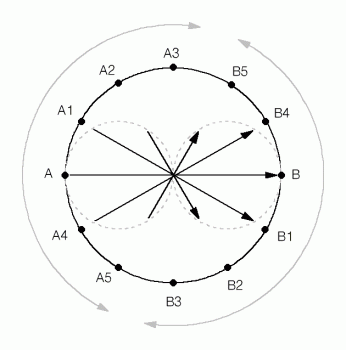
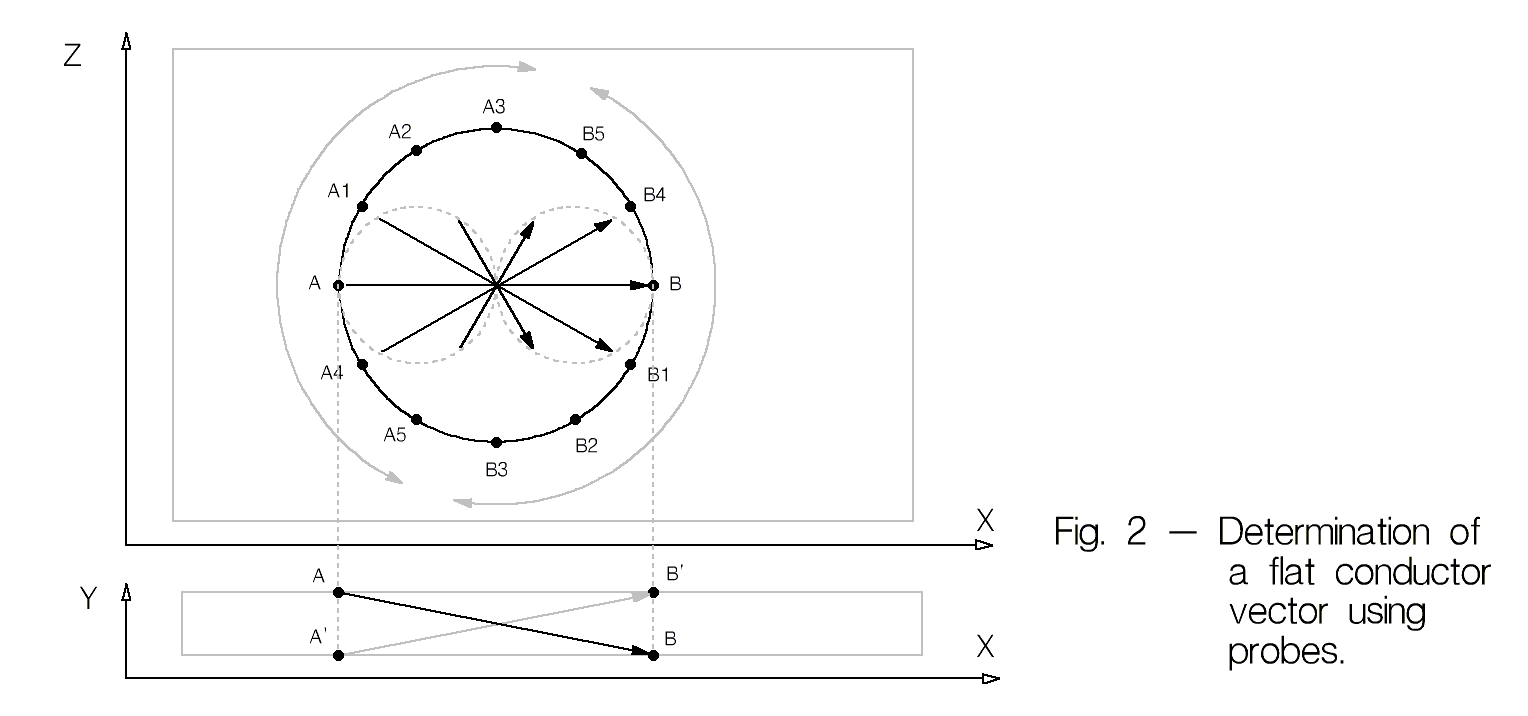
- При прочих равных, однонаправленные коллинеарные векторы звучат одинаково, таким образом, в каждом простом компоненте мы имеем бессчетное количество пар входных и выходных точек касания, с нулевыми векторными потерями. На рис. 5 \overline{AB} \equiv \overline{CD} \equiv \overline{EF} \equiv \overline{GH}
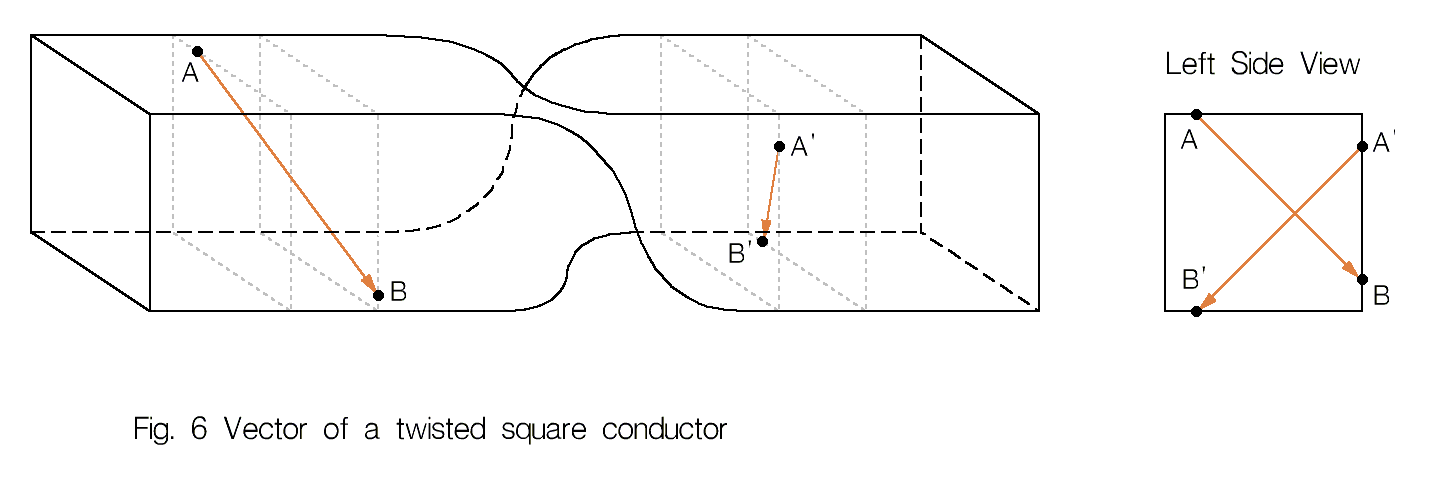
- При изгибе или скручивании моножильного провода, металлических пластин и т.п., их вектор изгибается и скручивается точно повторяя искаженную форму компонента (рис. 6), при этом, если затем восстановить форму компонента, направление его вектора так-же восстанавливается.
- Во направлениях, перпендикулярных вектору (см. рис. 2 нулевой вектор \overline{A3B4} ), направленность у компонента отсутствует, при этом звучание компонента становится усредненным по отношению к векторам \overline{AB} и \overline{BA} .
- Векторы не меняют свою ориентацию относительно геометрической формы радиокомпонентов, ни под действием постоянного электрического тока, ни под действием магнитного поля.
Данное утверждение базируется на тщательном исследовании старых, преимущественно довоенных радиодеталей: трансформаторов, кондесаторов, радиоламп, проводки электроприборов, как постоянного, так и переменного тока десятилетиями проработавших в одинаковых «электро-магнитных условиях». Проводники и диэлектрики из которых собраны бывшие в долгом употреблении радиокомпоненты, с точки зрения направленности, всегда были соединены без какой-либо системы, например: направление выводов трансформаторов практически никогда не совпадало с направлением их обмоток, а проводка, включая отрезки проводников из которых собраны радиолампы, резисторы и конденсаторы никогда не соответствовала Электрическим Контурам и содержала как прямые, так и встречные включения проводников.
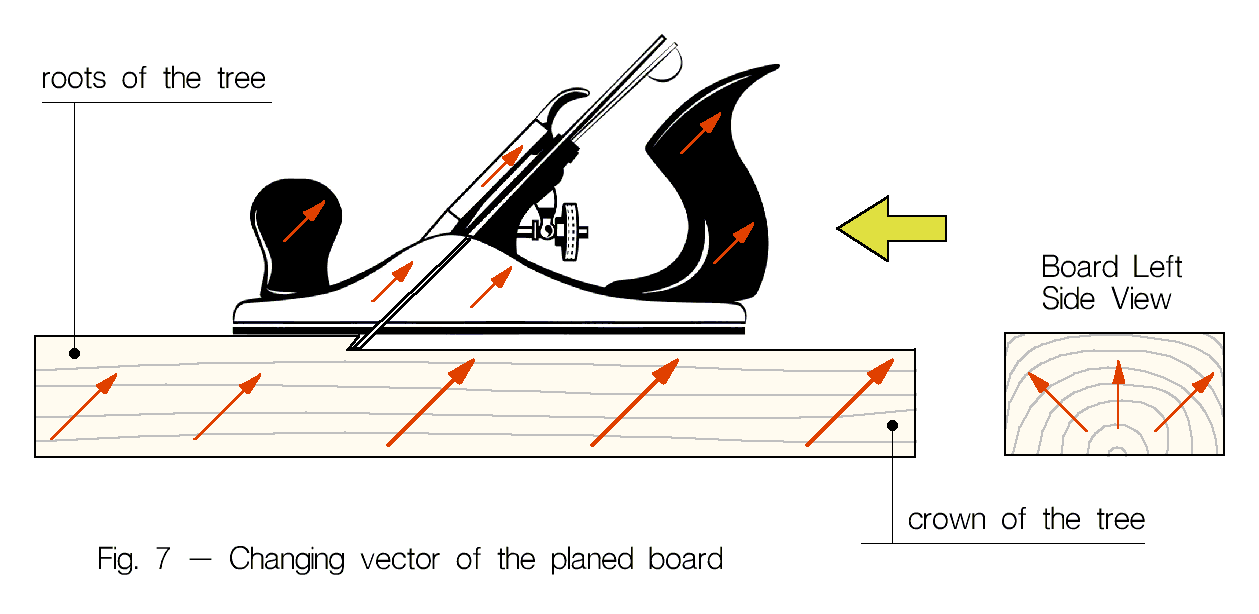
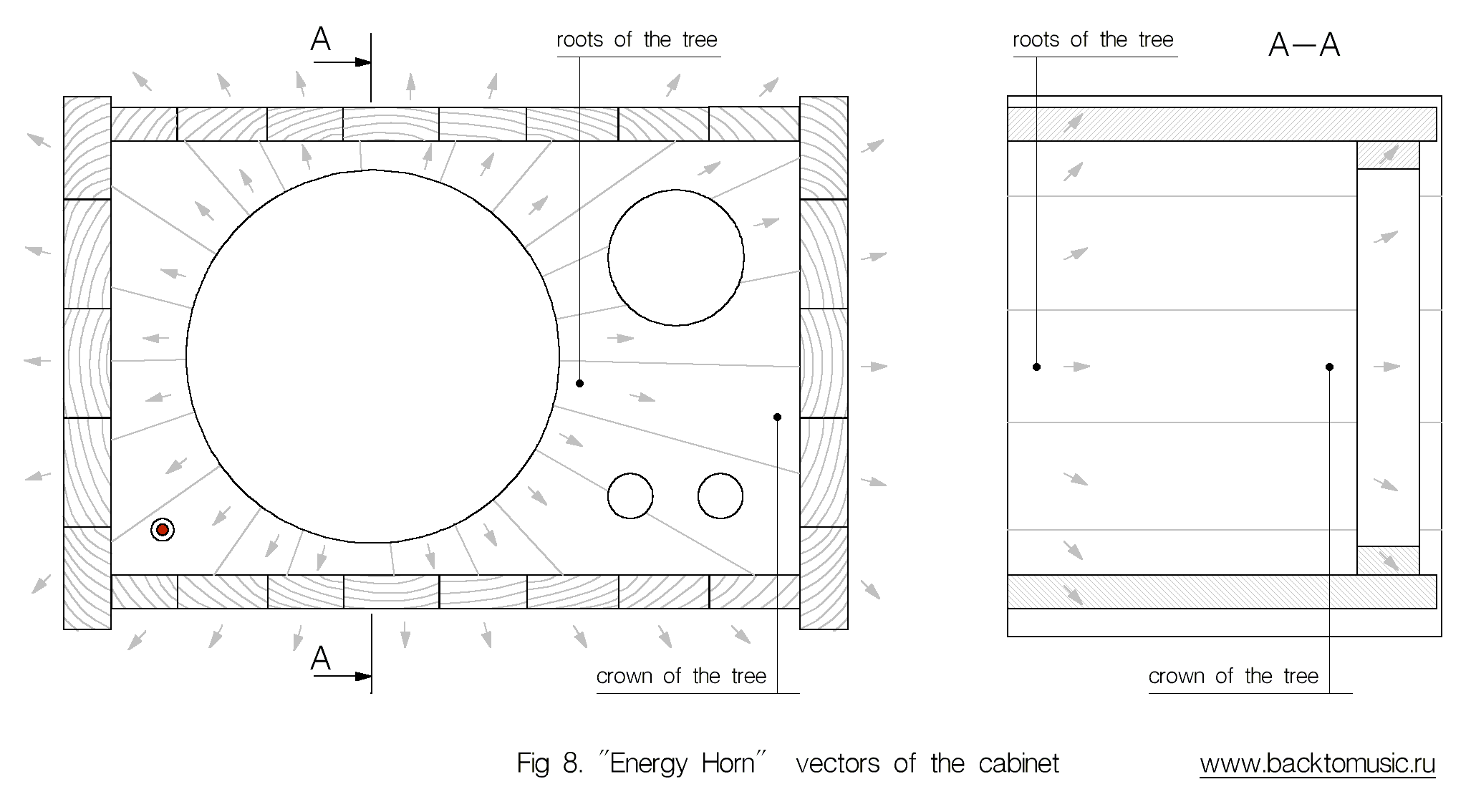
- Механическая обработка поверхности компонентов (пиление, строгание, шлифовка, етс.) вызывает коррекцию направления и силы Поверхностной Направленности (ПН). На рис. 7 показана правильная ориентация доски и рубанка при строгании: рубанок, доска и правая (входная) рука, толкающая рубанок, должны быть сонаправлены, только в этом случае во время обработки не возникают векторные потери ясности. Так же механическая обработка оказывает значительное и устойчивое влияние на неполярные, тонкие свойства компонентов (подробнее здесь).
- Направление и силу суммарного вектора группы компонентов можно оценить по математическим правилам сложения векторов отдельных компонентов, входящих в данную группу.
.
Вектор вращения
Вектор вращения (ВВ) определяет поступательное и тангенциальное направление навивки проводника относительно направления проводника и продольного направления детали, на которую навивается проводник. ВВ необходимо учитывать при намотке трансформаторов, катушек индуктивностей, проволочных резисторов, фольговых рулонных конденсаторов. Направление ВВ перпендикулярно плоскости вращения и связано с направлением вращения правилом правой руки.
 «Если взять правой рукой каркас катушки индуктивности так, чтобы выпрямленный большой палец указывал в сторону продольной направленности каркаса, то провод должен навиваться на каркас в направлении, указанном обхватывающими каркас четырьмя пальцами. Начало провода должно быть расположено у мизинца, катушка мотается в направлении от мизинца к указательному пальцу»
«Если взять правой рукой каркас катушки индуктивности так, чтобы выпрямленный большой палец указывал в сторону продольной направленности каркаса, то провод должен навиваться на каркас в направлении, указанном обхватывающими каркас четырьмя пальцами. Начало провода должно быть расположено у мизинца, катушка мотается в направлении от мизинца к указательному пальцу»Радиус Вектор
Радиус Вектор (РВ) образуется в многослойных катушках индуктивности и рулонах конденсаторов, в природе присущ всем растениям и направлен от центра наружу (см. рис 4). Для достижения максимально ясного звучания системы, РВ индуктивностей и конденсаторов так-же должен быть направлен от центра наружу. Чтобы сформировать Вектор с таким направлением, надо перед намоткой компонента убедиться, что в катушке, с которой вы будете сматывать провод или фольгу, снаружи находится начало провода (фольги). Если это не так, то катушку — источник провода надо перемотать на пустую катушку и только потом мотать обмотку будущего трансформатора или обкладку конденсатора. У фольги дополнительно определяется входная и выходная поверхности ( см. рис 2 — вектор плоского проводника), при намотке входная поверхность фольги должна располагаться ближе к центру рулона. Правило Радиус Вектора:
Формирование вектора с заданным направлением
В домашних условиях можно сформировать вектор у легкоплавких металлов (свинец, олово, алюминий), а так-же у диэлектриков (восках, смолах, лаках и красках). Так-же можно собрать из деталей с известной направленностью какой-либо предмет с необходимыми свойствами, например склеить корпус АС (рис. 8). На данный момент известно, что устойчивая, векторная направленность у металлов и диэлектриков формируется в момент их перехода из жидкого состояния в твердое, предположительно — под действием некого, направленного Векторного поля при этом компонент во время своего перехода из расплавленного состояния в твердое «запоминает» то состояние поля, которое его пересекало (окружало) в данный момент и «помнит» его до тех пор, пока его снова не расплавить. У человека (лично у меня) сильный и стабильный источник векторного поля — это руки. Степень влияния других частей тела варьируется под действием различных, плохо предсказуемых обстоятельств. Что-либо говорить о сознательном и целенаправленном применении тонких полей человека в аудио пока не представляется возможным, однако не подлежит сомнению, что человек оказывает ощутимое влияние на звучание конструкции, которую он изготавливает не зависимо от того, хочет он этого, или нет. Векторное поле каждого предмета, как и векторное поле человека, оказывает влияние на формирование направленности у находящихся рядом с ним предметов, которые в этот момент переходят из расплавленного состояния в твердое. Таким образом, можно говорить о наличии тонких, векторных полей разной силы и конфигурации у всех окружающих нас предметов. Влияние векторных полей предметов на формирование векторов у расположенных рядом с ними затвердевающих жидкостей, пропорционально их текущей силе и обратно пропорционально расстоянию между ними.
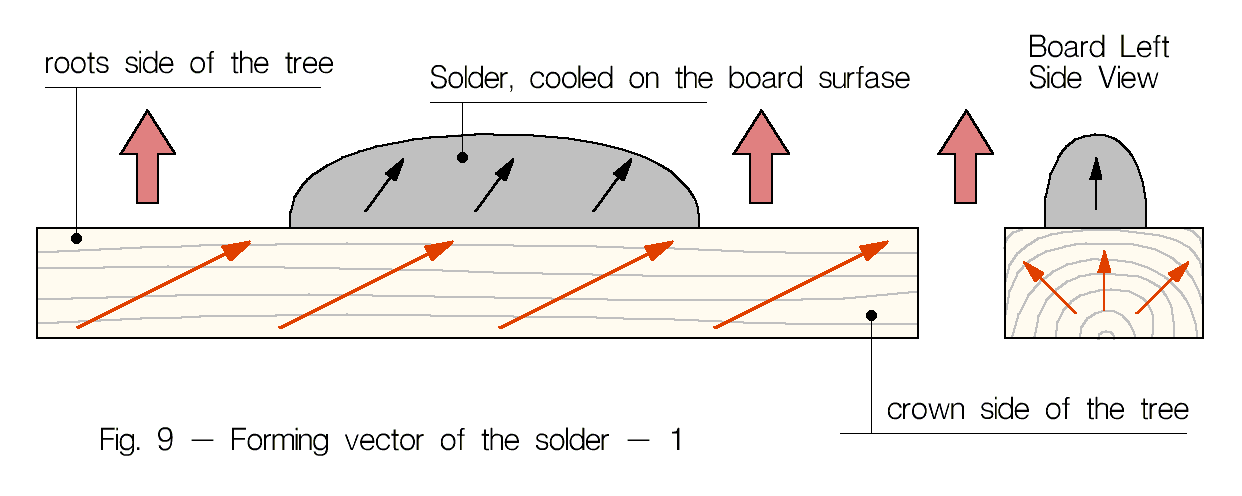
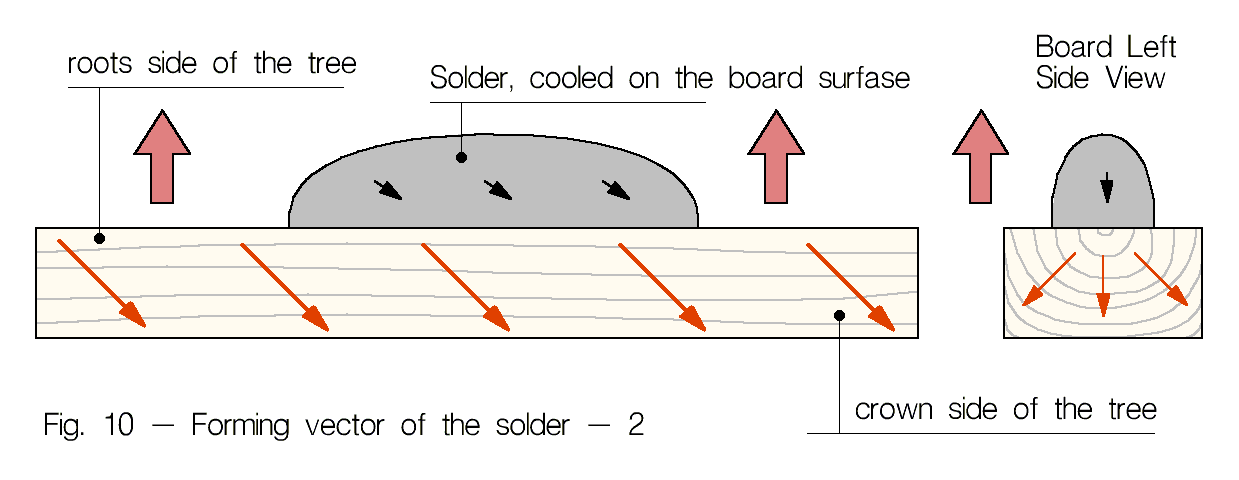
Существует, по крайней мере, один источник векторного поля, влияние которого не зависит от расстояния до какого либо объекта в помещении. Данное поле, в случае, когда ему не оказывает противодействие поля посторонних, близко расположенных предметов и/или человека, формирует у затвердевающих предметов устойчивый вектор с направлением «снизу-вверх». Наличие этого поля было выведено логически, когда стало ясно, что во время экспериментов по формированию направленности у радиокомпонентов, каждый раз отслеживается некая коррекция вектора в направлении «снизу-вверх». Скомпенсировать это влияние «снизу-вверх» (то-есть отклонить его в сторону или изменить на противоположное направление) можно только если припой застывает на массивной доске или куске металла вектор которых направлен вниз. Возможно, данное влияние «снизу-вверх» — это влияние векторного поля Земли. На рис. 9 и рис. 10 показано два варианта формирования вектора у капли припоя, застывающей на деревянной доске. Жирными красными стрелками показано поле Земли, обычными стрелками — векторы доски и припоя, после его застывания. Звук припоя на рис.10 получается не сформированным, мутноватым, правильное направление на нем определить сложно. Чистое звучание у припоя получится только в случае, если вектор предмета на котором припой застыл примерно совпадал с направлением поля Земли (рис. 9).
Вывод
Векторную Направленность можно смело назвать теорией, поскольку она объединяет разрозненные, субъективные факты (как слуховые, так и зрительные) в единую систему и объясняет плохую повторяемость многих субъективных экспериментов, позволяя сделать их более повторяемыми.
Примечания
[1] — см. мое интернет сообщение от 7 марта 2006г, (Логин для входа — oldforum, пароль — 159357) Цитата:
…Правильное направление имеет три независимые координаты по отношению к продольной оси у ЛЮБОГО проводника т.е. у полоски фольги есть входная и выходная сторона а цилиндрический проводник необходимо соединять определенным боком. Таким образом Вектор правильного направления стал трехмерным и сейчас исследуются способы минимизации векторных потерь…
[2] — Ссылка на источник не найдена.
[3] — см. мое интернет сообщение от 6 декабря 2006г, (Логин для входа — oldforum, пароль — 159357) Цитата:
…Есть еще немаловажные тонкости. Эти, найденные мной эзотерические правила, действуют и в головках и в трансформаторах и в рулонах конденсаторов и в динамиках — в любых радиокомпонентах, где есть спирали:
Катушка должна быть расположена вертикально (отверстие смотрит вниз),
Провод, если смотреть на катушку сверху, намотан по часовой стрелке.
«начало» провода должно быть внутри и сверху катушки. Заземляется именно начало провода. Конец провода становится сигнальным и он должен выходить из катушки внизу…

Здравствуйте Антон!
Давно хотел узнать Ваше мнение о влиянии резонансов в твердых материалах.
Твердые материалы можно условно разделить на резонирующие, демпфирующие и нейтральные, если так можно выразится. Примеры резонирующих — сталь, бронза. Примеры нейтральных — медь, дерево, стекло. Примеры демпфирующих — свинец, линолеум, войлок. Резонирующие материалы, как мне кажется, усиливают динамику звука, как-бы дифференцируют его и вносят более яркий окрас. Демпфирующие материалы делают звук более спокойным, интегрированным, в чрезмерном случае — «зажатым», их окрас менее заметен, и они, возможно, даже давят окрасы материалов соседствующих элементов конструкции. Нейтральные материалы — нечто среднее, вроде-бы, золотая середина.
Все куски этих разных материалов, разумеется, имеют свои вектора направленности. Что в них различного в плане теории ВН? Разная проводимость тонкой энергии звука?
Как Вы думаете, как лучше использовать разнообразие материалов по резонансной способности? Казалось бы, демпфирующие материалы хороши для механического разделения разнонаправленных деталей, т. е. они являются приближением к воздушным промежуткам?
Если резонирующие материалы наиболее эффективно передают тонкую энергетику, то, видимо, преимущественно, конструкцию нужно выполнять из них, прокладывая демпфирующие материалы в тех соединениях, где ВН невозможно согласовать? Или, оптимальным будет использование нейтральные по резонансам (апериодические) материалы? Или это все мои заморочки и не нужно обращать внимание на резонансы и демпфирование, а учитывать только красоту окраса и направления?
С точки зрения ВН различия в них нет. Все они имеют направленность, которую желательно соблюсти дабы их звук стал ясным и мелодичным в максимально возможной степени для данного, конкретного компонента.
На слух выбираем лучшее из того, что имеем.
К сожалению нет. Систему приходится складывать из максимально сонаправленных деталей, включая демпферы. Любые разнонаправленные касания в той или иной степени портят звук .
В электрической части имеет смысл обращать внимание только на окраску и направленность. Если речь идет о механике, например о звукоснимателе или громкоговорителе, то там конечно надо сечь резонансы и при необходимости демпфировать их, соблюдая при этом направленность демпфера. Но демпфировать резонанс без потерь ясности обычно не удается, так что тут всегда приходится идти на компромисс.
Антон. спасибо за пояснения! То что демпфирование портит звук я неоднократно убеждался. В противовес демпфированию, иногда используют специальные конструкции, разбивающую один большой резонанс на несколько, разнесенных по частоте с меньшими амплитудами. Например, в известных колонках от радиолы «Симфония» внутренний объем разбит на 3 камеры, сообщающихся небольшими отверстиями. При этом, один резонанс разбивается на три, разных по частоте и меньших по амплитуде. Но это — усложнение конструкции, что противоречит идее короткого пути. Хотя, наверное, разбиение одного мощного резонанса на несколько небольших резонансов предпочтительнее по сравнению с демпфированием.
Наверняка сказать нельзя, все будет зависеть от реализации.
Собрал вместе разрозненные по сайту сведения о векторах, добавил иллюстрации, постарался все расписать максимально понятно.
Антон, более трёх лет назад я описал ( ссылка: http://www.shabad.ru/forumaml/showthread.php?t=3369 ) проделанный мной несложный эксперимент. Эксперимент касается направленности проводников.
Можете повторить его и сообщить своё мнение?
Я давно хотел обратиться к Вам, но решился вот сейчас.
Александр, я ставил опыты по отжигу и много чего другого. По моему опыту направленность вообще неустранима, она обнаруживается всегда и во всех предметах, простых и сложных, металлах и диэлектриках. Устранение направленности, на мой взгляд, — это нонсенс. Не вижу смысла проводить такие опыты.
По вашему направленность есть только в рафинированных проводах и объясняется нелинейностью таких проводов, или я что-то не уловил?
«Александр, я ставил опыты по отжигу и много чего другого. По моему опыту направленность вообще неустранима, она обнаруживается всегда и во всех предметах, простых и сложных, металлах и диэлектриках. Устранение направленности, на мой взгляд, — это нонсенс. Не вижу смысла проводить такие опыты.»
Антон, я правильно понимаю, что речь идёт исключительно о твёрдых материалах?
Если да, то я с Вами был в основном согласен и жил спокойно.
К моменту проведения моего эксперимента из моего предыдущего опыта мне было известно следующее. (С некоторым упрощением и из тех проводов, которые мне были доступны для прослушивания.)
1. Среди древних проводов есть более ясно «звучащие» относительно других.
Среди современных проводов есть более ясно «звучащие» относительно других.
Но самый ясно звучащий современный провод звучит менее ясно, чем самый неясно звучащий из древних.
2. Наиболее ясно звучащий провод имеет наименее выраженную направленность. (Мне казалось это принципиально важным)
3. При отжиге провода звук меняется, на мой взгляд, в лучшую сторону. Но направленность остаётся.
4. А так же, из проведённого Вами в стародавние времена опыта с расплавленным припоем, что направленность можно менять. (Тогда не пришло в голову проверить эффект после вращения капли припоя во время застывания. Но я повторил его с пропусканием белого шума.)
Так получилось, что в те дни, когда я читал книгу Ф. Вильчека «Красота физики», из неё как раз в моём сообщении на АМЛ форуме приведены две формулы, мне на YouTube попался ролик, в котором демонстрировалось, что пламя свечи является проводником тока. И эти не связанные между собой, и с интересующей меня проблемой ясности и направленности, натолкнули меня на мысль о проведении того эксперимента.
Повторили эксперимент только двое Сергей Банковский и Аббас Зульфугаров. Первый отозвался в целом положительно, а второй отрицательно. Но в его (Аббаса) сообщении есть фраза: «Если в проводе остаются не отожженые участки, он сохраняет первоначальную яркость.»*, противоречащую всему сказанному о проведённом им эксперимента. Т.е. отожжённый участок никак не влияет на звучание ярко звучащих не отожжённых концов, т.е. превращается в перемычку. И осталось не ясным, как он тогда так сильно влияет на весь тракт что:
«1. Блеск и металл из голоса заметно уходят, звук из за этого становится менее естественным, блеклым ( это значит, что в результате обработки провалена высокая певческая форманта).
2.Специально слушал качество баса- бас фортепиано несколько потерял наполненность и весомость удара, будто из молоточка убрали массу. Бас стал скучным и пустотелым.
3. Энергетика человеческого голоса заметно ослабевает. Он становится старческим и вялым.»*
Там же: «Оба образца сохранили направленность, но под шумом она ещё более невнятная.»*
Что значит невнятная? Трудно различимая? Всё-таки провод теряет направленность, пусть и не до конца?
*Фраза взята от сюда: https://abbasaudio.listbb.ru/viewtopic.php?f=19&t=2545&st=0&sk=t&sd=a&hilit=провод+до+красна&start=100
Больше никто не повторил ни на форуме Шабада, ни на форуме Аббаса.
Вообще говоря, выводом, сделанным после проведения эксперимента, я подверг сомнению Ваше утверждение: «направленность вообще неустранима, она обнаруживается всегда и во всех предметах, простых и сложных, металлах и диэлектриках».
И предложил способ проверки. Поэтому мне кажется, Вам следует, проведя эксперимент либо опровергнуть мой вывод и укрепить своё утверждение, либо скорректировать своё утверждение.
По крайней мере, так принято в научных кругах, т.е. там, где стремятся понять или хотя-бы приблизится к пониманию истины.
Впрочем, у меня нет оснований на чём-либо настаивать.
«По вашему направленность есть только в рафинированных проводах и объясняется нелинейностью таких проводов, или я что-то не уловил?»
Про нелинейность ничего сказать не могу.
У старых проводов направленность присутствует.
Также я заметил, что с железными и серебряными проводами подобного не происходит.
И предположил, что такой же эффект должен быть у проволоки из хрома. Но проволоку найти не удалось, чтобы проверить.
Да. В жидкостях померить направленность нельзя по определению, однако я давно обнаружил и использую способность жидкостей (капли воды или спирта) передавать направление твердого диэлектрика, на котором эта капля находится. С помощью спирта например можно определить направление пластины кристалла сегнетовой соли от пьезокартриджа. Капаешь каплю-другую на поверхность, а потом щупами тестового аудиотракта с большим входным сопротивлением определяешь вектор, как обычно у проводника.
Александр, с отжигом все сложнее, чем вы пишете. Гораздо сложнее. Результат эксперимента будет зависеть от
— источника пламени (газ на кухне испортит звук хорошего провода, еще больше пострадает отличный, открытый огонь может улучшить хороший, но отличный опять же скорее всего ухудшит какие то свои параметры. Плохой провод при этом можно улучшить до хорошего.
— соблюдения определенного положения провода по вертикали относительно его направленности.
— Оценивать результат опять же надо с учетом вектора провода, иначе разница в звучании даже одного и того же отрезка провода будет плавать в широких пределах.
Это только то, что лежит на поверхности. В процессе проведения любых подобных экспериментов обязательно всплывают дополнительные трудности в получении устойчивого, повторяемого хотя бы на 80-90% результата. Необходимые перепроверки каждого шага сами по себе могут давать ошибки, я сталкивался с таким не раз. Это я пишу, чтобы объяснить мое нежелание проводить трудоемккий эксперимент и перепроверять результат изначально не корректно поставленного эксперимента. При этом я вполне уверен в том, что с направленностью твердого предмета по большому счету ничего сделать нельзя, если только не переплавить металл. Еще напомню — направленность присутствует в диэлектриках, как искусственных, так и природных, в самородках графита и тд, здесь она никак не может получаться с помощью токов каких-то шумов или нагрева докрасна. Соответственно, надо искать причину возникновения (существования) направленности в другом месте, искать что-то, что одинаково влияет на проводники и диэлектрики, а не терять время на эксперименты, которые по своей сути не могут объяснить точную причину. Последняя причина — главная, почему мне в принципе не интересны отжиги, неважно под током или без.
Цитаты выделить не удалось.
На картинке мое предыдущее сообщение с цитатами, которое я писал в текстовом редакторе. Сообщение было скопировано, вставлено в окошко на сайте и отправлено как есть. Как можно видеть, все, что внутри тэгов «blockquote» сайт отформатировал, как цитаты.
Понял. Нет так нет.
Вопрос. А Вы не пересмотрели своё утверждение, что можете формировать направленность расплавленной капли припоя во время застывания?
В этот раз получилось. В предыдущий раз я оставлял пробел перед и после текста.
Влияние есть однозначно! Другое дело, что сейчас я не уверен в том, что именно (какая часть тела) и каким образом это получается. не могу придумать чистый эксперимент, да в общем и не думаю над этим уже давно. Там чем дальше в лес, тем больше нюансов возникает, которые надо учитывать, в итоге неизвестных оказывается слишком много для какого либо вывода.
Единственное, что я использую сознательно — это влияние «поля Земли» если я паяю два провода, то выходной всегда располагаю над входным. Это работает однозначно.